A Practical Algorithm for Surface/Surface Intersection

Ling Huang   Xinxiong Zhu

（School of Mechanical Engineering & Automation,

Beijing University of Aeronautics & Astronautics, Beijing, 100083）

 

Abstract:  A practical solution to the surface/surface intersection is presented. This algorithm combines the techniques of loop detection, point marching and curve approximation, etc. Given a set theoretical curves constrained by surface/surface intersection equations, the algorithm can get all the intersection branches, and construct spline curves to approximate every theoretical curve with least data in terms of the given tolerance.

1.  Introduction

The problem of computing the surface/surface intersection (SSI) curves is a fundamental one in CAD/CAM. It arises from a broad spectrum of tasks, ranging from solid topology operation to manufacturing processes.

Given two surfaces  and , there would possibly be a parametric equation  which exactly expresses the theoretical intersection curves of those two surfaces:

                                                   (1)

However, algebraic degree and genus of the intersection curves are so high that even an SSI curve of two bicubic patches cannot be expressed precisely by using rational polynomial parametric equations, for only curves with genus being zero have an exact parametric equation. In general, numerical solutions are necessary and SSI curves can be approximated by using parametric curves, for example, by NURBS.

For surface/surface intersection, the divide-and-conquer algorithm and the marching algorithm are commonly used. In subdivision based algorithms, the surfaces are subdivided into a great number of facets and the intersection of surfaces is approximated by the intersection of the facet pairs. Marching algorithms begin by finding one starting point on the intersection curve and marching along the curve to get the successive points. But they are inefficient to deal or incapable to dealing with the singular cases (for example, tangent or overlap of two surfaces). Hence, it is very hard, if not impossible, to obtain all the intersection segments (for example, the small intersection loops) in an SSI algorithm.

In commercial CAD/CAM systems, an SSI algorithm should be able to obtain all the intersection curve(s) steadily and exclusively. And, the result curve(s) approximated by NURBS should be within the given tolerance. The practical solution for surface/surface intersection should be the combination of many techniques.

This memorandum presents a practical solution to the surface/surface intersection which combines the techniques of loop detection, point marching, curve approximation, etc. Given a set theoretical curves constrained by surface/surface intersection equations, the goal of the algorithm is to get all the intersection branches, and constructs a NURBS curve to approximate every theoretical curve with least numbers of segments in terms of the given tolerance. All the curves can be found by obtaining an initial marching point for every branch and all the points and tangent vectors on every curve can be calculated.

 

2.  Strategy

2.1  Procedure

The main steps of our surface/surface intersection algorithm can be summarized as follows:

l       Step1: Obtain a starting point for every intersection curve by exploiting the plane vector field method.

l       Step2: March along every intersection curve steadily to get the successive intersection points with an adaptive step length calculated by taking advantages of the local curvature of the curve.

l       Step3: Calculate the significant points on every intersection curve in the marching process and partition the curve to a number of monotonic intervals.

l       Step4: Construct a NURBS curve fitting the sample points (including significant points and all the marching points) and get a candidate approximation curve for every theoretical intersection curve.

l       Step5: Estimate the deviation between the candidate NURBS curve and the theoretical curve in every interval and check if the deviation is within the given tolerance.

l       Step6: If all the deviations are within the given tolerance, the candidate NURBS is accepted. Otherwise, add new marching point(s) into the sample points array in the interval(s) where the deviation exceeds the given tolerance. Go to step 4.

2.2  Obtaining Starting Points

The most difficult problem in surface/surface intersection is to find all the intersection curves without missing any one. The intersection of two surfaces may include two types of curves: (1) closed loops and (2) open branches, as shown in Fig.1.

 

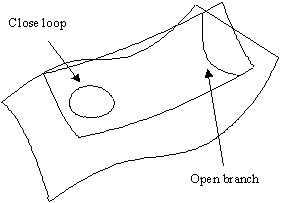
Fig.1  Types of intersection curves.

It is easy to locate a starting point on an open branch by simply intersecting all the boundary curves of each patch with the opposing patch. On the other hand, if closed loops exist, there is a major challenge in surface intersection algorithm. There are many different ways to solve this problem, including patch subdivision and loop detection.

      In our method an algorithm based on the theory of plane vector field is exploited to obtain the starting points of all the intersection curves. The key of intersection finding is relevant to the global searching and local positioning of intersection area. And, the theories of topology and differential geometry provide the base to solve the problem. It is convenient to express an intersection curve as a set of points on the two surfaces with zero distance which results in the oriented distance function of one surface from the other. The gradient of the oriented distance function defines a vector field that is useful in solving the parametric surfaces intersection problems. An adaptive method in terms of Poincare index was developed that invoked the rotation number of vector fields to find the critical points of the oriented distance function between two parametric surfaces. This approach allows the development of a global method for identifying the areas enclosing small loops and significant points of the intersection set. Many papers discussed this method in detail and can be exploited.

2.3  Point Refinement

       Initial approximated points, either starting points or marching points should relax onto the intersection curve by Newton-Raphson iteration.

      Given an approximate intersection point , and candidate parameter pairs of surfaces  and  of . In general, point  will not lie on either surface. The method for point refinement is first to obtain surface “near points”, which are the points on surface and  with a minimum distance from , as shown in Fig.2.

 

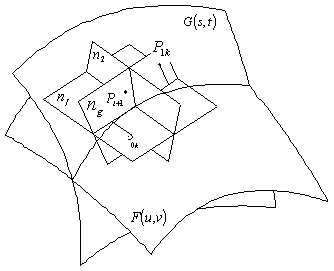
Fig.2  Point refinement

As shown in Fig.2, projecting the midpoint of the surface near points  and  onto the intersection line of the tangent planes can get the next iterative point. With  and  as the normals at the near points on surface  and , and with  as the third one, the point  for next iteration can be calculated by Equation 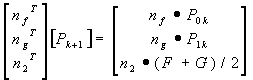(2):

                                             (2)

Then, the Newton-Raphson iterative equation set follows:

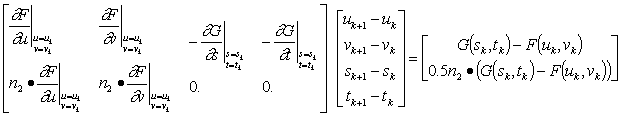
(3)

This process continues iteratively until it converges.

       Alternately, the equation set of intersection  can be handled directly by specifying a constant domain parameter as an additional constraint. This idea can be used to relax boundary points onto surface boundaries. For example, at  or  boundary on surface , it would be possible to incorporate the  constraint directly into the system and a new iteration being a 4 by 4 system with 4 unknowns can obtained. For example, at  boundary the system is:

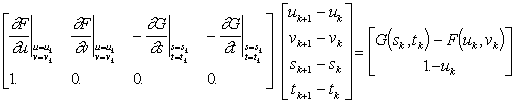               (4)

In trimmed-surface intersection, iteration on trimmed boundaries should be dealt with. This becomes a problem of curve/surface intersection. For example, on trimmed boundaries of surface  denoted by parametric curve , the iterative equation set is:

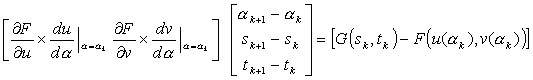           (5)

2.4  Marching along Intersection Curves

      After finding out a point on every intersection curve, successive intersection points can be generated by going a step in the direction defined by the local differential geometry of the curve. It is also necessary to determine the step length at which a new approximative point is obtained. If a step length is too big the intersection approximations may be wrong and the point refinement may not converge; if it is too small, the efficiency of the algorithm decreases. We use an adaptive step length approach based on local curvature at the intersection point.

For the tangent planes of two surfaces are not parallel, step vector directions can be calculated by the cross product of the surface normals. If surface tangent planes are coincide, the normal curvature is employed to calculate the marching direction. In this case, marching direction is the direction where two normal curvatures of the surfaces are equal and can be calculated by Euler formula.

       With a step direction known, an adaptive step length is calculated based on the approximate curvature and chord tolerance . An osculating circle is approximated at a given point  to obtain the radius of curvature. The circle is defined by  and its precedent , and the unit step vectors  and on them. The approximated radius of curvature is:

                                                         (6)

As shown in Fig.3, the step length can  be calculated by Equation (7):

where                                                                                          (7)

 

 

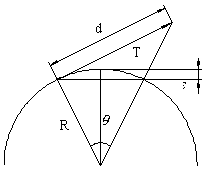
Fig.3  The step length

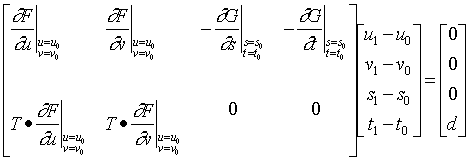Then, the next approximate intersection point , and the candidate parameter pairs () and () of surfaces  and , can be calculated in terms of current point  with  parameter pairs and  by Equation (8):

                           (8)

where  is the step vector  and is step length. By Equation (3), point  can be relaxed onto the intersection curve and the “real” intersection point can be obtained. If the Newton-Raphson  iteration  for  does not converge, the step length  should be reduced until the iteration converges (It is always possible to make it converging by making sufficiently small).

2.5  Calculating Significant Points

The significant points on intersection curves, such as Border_Points, Turning_Points and Cusp_Points, subdivide the curves into many monotonic intervals and reflect the overall shape of the curves, as shown in Fig.4. These points are crucial to the marching process and keeping consistency of the topology of the intersection curves. Also the significant points are important and helpful to the processing of curves approximated by NURBS.

The significant points on surface  can be defined as follows:

l       Turning_Points conditions in u-direction:

 and                          (9)

l       Turning_Points conditions in v-direction:

 and                    (10)

l       Cusp_Points conditions:

                                                                   (11)

where  is the normal vector on surface . Similarily the significant points on surface  can be defined. Assume that current intersection is , the next marching point is  and the domain value tuples of  and  are  and , respectively.

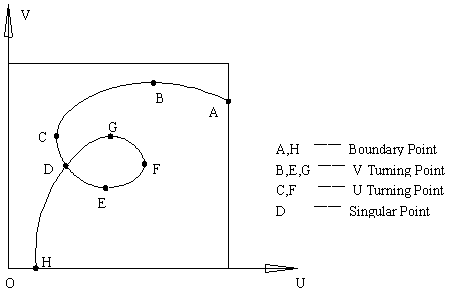
Fig.4  Significant points on intersection curves

      The significant points can be detected in the marching process as follows:

       If ( or  or  or ), there is a Turning_Point or a Cusps_Point betweeen  and .

       If ( and  and  and ), there is a Cusps_point between  and .

       where

，

，

，

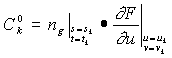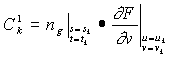
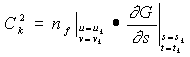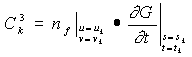
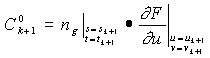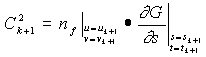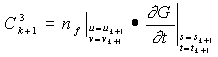，            (12)

If there is(are) significant point(s) in interval , the interval should be subdivided gradually to locate the significant point(s).

2.6  Approximating Intersection Curves by NURBS

      Theoritically, finding a starting point and marching along the curve with the marching step small enough, we can get all the points and it’s first derivatives for every curve. With the given chord tolerance  getting smaller, enough intersection points can be obtained to reflect the overall shape of every intersection curve generated by marching procedure. Those points, sampled from the theoretical intersection curves, serve as the point array for constructing the initial candidate NURBS by fitting (interpolation or approximation) technique.

       Obviously, the candidate NURBS curve goes through those points precisely or approximatively and the deviations between the candidate NURBS curve and the theoritical one at those points are within given tolerance. So we should only estimate the deviation in the corresponding interval(s).

       For convenience, we can consider that the maximum deviation in every interval is located at the point where the parameter value tuples on two surfaces is the average of those corresponding to two interpolating points. For example, in interval between points  and  with the parameter value tuples being  and  on two surfaces, respectively. Then the approximative  intersection point  to estimate deviation can be obtained with candidate parameter value tuples  on two surfaces. Relaxing point  onto the intersection curve and projecting it to the candidate curve,  the maximum deviation in interval  can be obtained. And, the maximum deviation of all intervals can be calculated. If the maximum deviation is less then the given tolerance, the procedure stops and the candidate NURBS curve is the right one. If the deviation(s) in some interval(s) exceed(s) the given tolerance, new intersection points, for example , should be added into the point array. Estimating all the deviations interval by interval, adding the point(s) into the point array and repeating the procedure, we can get the candidate NURBS curves with less and less deviation. The procedure goes repeatedly until a satisfied curve is obtained.

3.  Samples

      The algorithm has been used to a number of cases in surface/surface intersections, including blending two surfaces, trimming a surface by another surface, etc. The algorithm has been realized by ourselves with C and C++, and incorporated into our commercial CAD/CAE/CAM software system —CAXA-ME. Fig.5 through Fig.9 show that the algorithm is feasible, stable and efficient.

             

 

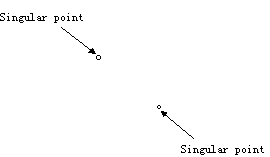
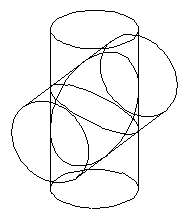
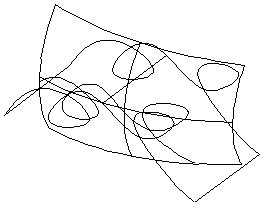
Fig.5  Intersection curve with singularities         Fig.6  Intersection curve with self-intersection

 

 

              

 

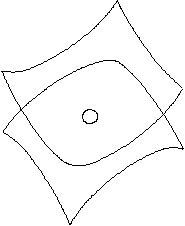
  Fig.7 Surfaces intersection with small loop           Fig.8 Surfaces intersection with many branches

 

References:

[1]    Houghton E.G., Emnett R.F., Factor J.D. and Sabharwal, C.L., Implementation of a divide-and-conquer method for intersection of parametric surfaces, CAGD, 2, 1985, 173-183.

[2]    Barnhill R.E. and Kersey S.N., A marching method for parametric surfaec/surface intersection, CAGD, 7, 1990, 257-280.

[3]    Sederberg T.W. and Nishita T., Geometric Hermite approximation of surface patch intersection curves, CAGD, 8, 1991, 97-114.

[4]    Sederberg T.W., Christiansen H.N. and Katz S., An inproved test for closed loops in surface intersections, CAD, 21, 1989, 505-508.

[5]    Cheng K.P., Using plane vector fields to obtain all the intersection curves of two general surfaces, in Strasser W. and Seidel H.(Eds.) Theory and practice of Geometric Modeling, Springer-Verlag, New York(1989), 187-204.

[6]    Kriezis G.A., Patrikalakis N.M. and Wolter F-E, Topological and differential-equation methods for surface intersections,  CAD, 24, 1992, 41-55.

[7]    Yawei M. And Luo R.C., Topological method for loop detection of surface intersection problems, CAD, 27, 1995, 811-820.

[8]    Ning Tao, The Research on Application Technologies of NURBS Surface Modelling,, PhD Thesis, Beijing University of Aeronautics & Astronautics, 1995.

[9]    Farouki R.T., The Characterization of parametric surface sections, Computer Vision, Graphics, and Image Processing, 33,1986, 209-236.

[10] Wang E.L., Gursoz J.M., Chen F.B. and Patrikalakis N.M., Intersection of parametric surface for next generation geometric modeler. In Turner J., Pegna J. And Wozny M., eds. Product Modeling for Computer-Aided Design and Manufacturing, 1991, 75-96.

[11] Huang Ling, Approach for Approximating Arbitrary Curves by NURBS, HZ-TMSurf-Huang01, BUAA, 1995.